
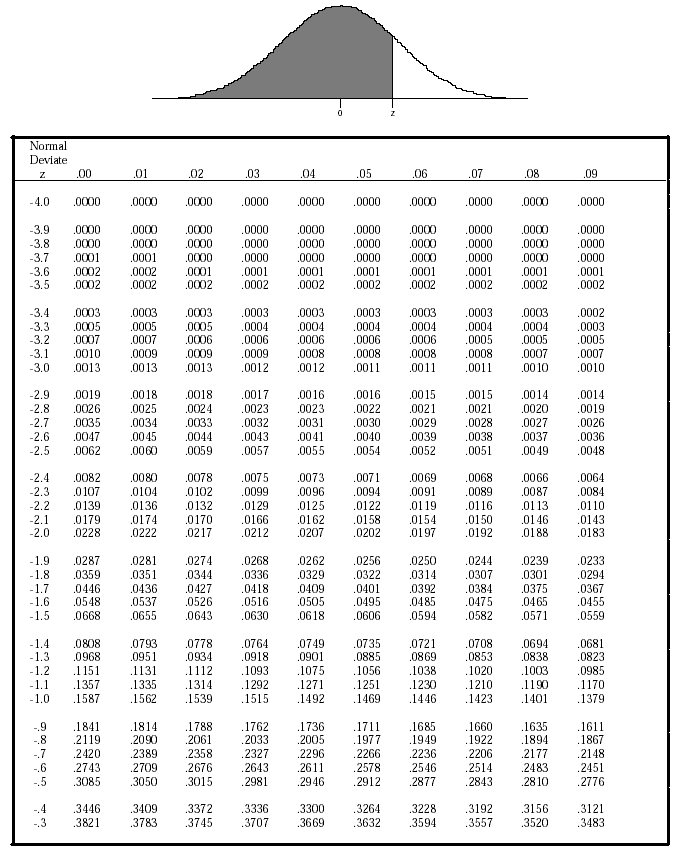
Statisticians standardize many measures by using the standard deviation. In order to see that so many things have the same normal shape, all must be measured in the same units (or have the units eliminated)-they must all be standardized. If you are a skeptic, you are wondering how can GPAs and the exact diameter of holes drilled by some machine have the same distribution-they are not even measured with the same units.

The normal distribution really is a normal occurrence. In human performance, scores on objective tests, the outcomes of many athletic exercises, and college student grade point averages are normally distributed. In manufacturing, the diameter, weight, strength, and many other characteristics of human- or machine-made items are normally distributed. In nature, the weights, lengths, and thicknesses of all sorts of plants and animals are normally distributed. Statisticians have found that many things are normally distributed. Most of the members of a normally distributed population have values close to the mean-in a normal population 96 per cent of the members (much better than Chebyshev’s 75 per cent) are within 2 σ of the mean. Normal distributions are bell-shaped and symmetric. The immediate goal of this chapter is to introduce you to the normal distribution, the central limit theorem, and the t-distribution. These ideas will be developed more later on. By assuming that the sample is at least fairly representative of the population, the sampling distribution can be used as a link between the sample and the population so you can make an inference about some characteristic of the population. The samples will vary, some being highly representative of the population, most being fairly representative, and a few not being very representative at all. Remember that the sample you are using to make an inference about the population is only one of many possible samples from the population.

Briefly, the general model of inference-making is to use statisticians’ knowledge of a sampling distribution like the t-distribution as a guide to the probable limits of where the sample lies relative to the population. Since you will be learning to make inferences like a statistician, try to understand the general model of inference making as well as the specific cases presented. The way the t-distribution is used to make inferences about populations from samples is the model for many of the inferences that statisticians make. The t-distribution and the central limit theorem give us knowledge about the relationship between sample means and population means that allows us to make inferences about the population mean. In between discussing the normal and t-distributions, we will discuss the central limit theorem. This makes the t-distribution useful for making many different inferences, so it is one of the most important links between samples and populations used by statisticians. It turns out that t-statistics can be computed a number of different ways on samples drawn in a number of different situations and still have the same relative frequency distribution. The relative frequency distribution of these t-statistics is the t-distribution. For each sample, the same statistic, called the t-statistic, which we will learn more about later, is calculated. The t-distribution can be formed by taking many samples (strictly, all possible samples) of the same size from a normal population. This chapter will discuss the normal distribution and then move on to a common sampling distribution, the t-distribution. If you ever took a class when you were “graded on a bell curve”, the instructor was fitting the class’s grades into a normal distribution-not a bad practice if the class is large and the tests are objective, since human performance in such situations is normally distributed. The normal distribution is the bell-shaped distribution that describes how so many natural, machine-made, or human performance outcomes are distributed. It is normal because many things have this same shape. The normal distribution is simply a distribution with a certain shape.


 0 kommentar(er)
0 kommentar(er)
